Already a quarter of the way through AoC! I’m taking off the week before Christmas so that I can burn some of my unused vacation time and maybe work on some of the really gnarly puzzles I know are coming.
This one, though, was easy. I solved it last night before I went to bed, in Python, using brute force. I rewrote it using quadratic equations before work, and have been fiddling with it for a few minutes.
The AoC subreddit is adding some extra challenges to the puzzle. Today was doing it on super old hardware or using a super old computer language. Now, I used to know COBOL, FORTRAN, Pascal and such back in the day, but those days are long gone. I toyed with trying to get one of those old languages running but I would have had to learn the languages all over again, so I decided just to go back to my first PC — the Atari 800 home computer and it’s BASIC cartridge.
I loved that thing. I mostly used FORTH to program it with, but that’s just another language I have forgotten over the years, so BASIC it was. My first computer language. They say you never forget your first… computer language… and I guess that’s so.
Today’s puzzle was all about racing toy boats. Why? Well, you can read all about it. To race these boats, you charge them by holding a button for a certain amount of time. When you let it go, it races ahead at a speed proportional to how long you held the button down. The race only lasts a certain amount of time, so you have to balance how long you charge it with running the race. Now to win the race, you have to beat the previous record.
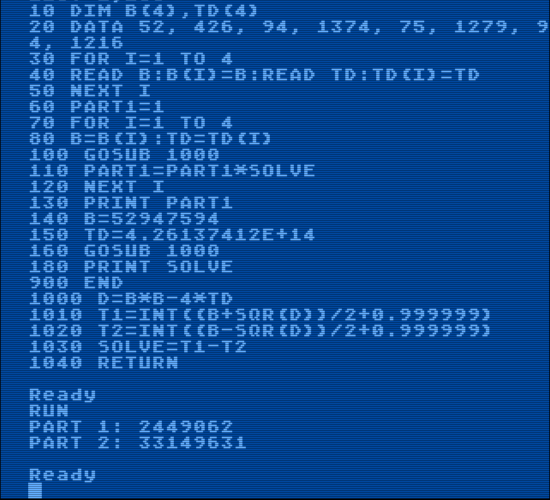
If the time the race lasts is t, and you hold the button down for x time units where 0 <= x <= t, then the final distance d is x(t – x) — this is a quadratic equation. We also need to beat the previous record, so we want to solve the equation such that we determine the times x which are the minimum and maximum amount of time we could hold down the button and beat the record. So the equation we are solving is x2-tx+d=0, where t is the total time of the race and d is the previous record. Subtract the (integral parts of) the low solution from the high solution, take the product of all four races, and that’s Part 1.
In Part 2, you smoosh all four race times together to make one huge number, and all four race distance records together to make one even huger number, and solve the equation for that, and that’s it, that’s the puzzle.
This was run on an emulator. I don’t know what happened to my Atari 800. Probably lost it when I moved to San Diego and we were cleaning out the house. I lost so much classic computer stuff. I keep wanting to buy another one, but realistically, it would just gather dust.
Eagle eyed reviewers might notice the output doesn’t match the program. Yeah, I changed the program and reran it and pasted the nicer output over the other stuff because I was lazy and had already stitched the program itself together — it wouldn’t all fit on one screen. I kinda thought I would have it graph the equation but I didn’t think it would really be worth learning how to do that all over again just for this.
If you want to see it in Python, who could blame you?
from math import prod, ceil
puzzle = [(52, 426), (94, 1374), (75, 1279), (94, 1216)]
def solve(time_distance: tuple) -> int:
b = time_distance[0]
d = (b**2) - (4*time_distance[1])
return ceil((b + d**0.5) / 2) - ceil((b - d**0.5) / 2)
def combobulate() -> tuple:
l = int(''.join([str(s[0]) for s in puzzle]))
r = int(''.join([str(s[1]) for s in puzzle]))
return (l, r)
print ("Part 1:", prod([solve(td) for td in puzzle]))
print ("Part 2:", solve(combobulate()))Since the input was so small, I just incorporated it into both of the programs and saved worrying about parsing.