Advent of Code Day 10 — Pipe Maze

Midjourney was entirely unable to render a picture using the holiday card style I’d generated, so I removed that constraint and told it to use its best judgement today to render a repairman in a metal world of pipes and mazes. Dall-E 3 did a better job with what I asked for, but Midjourney’s response was so creepy and cool that it had to be the header image.

So, here we are on the Metal Island, hang glider having successfully soared on thermals from the Desert Island, which is something I am not sure hang gliders can do, but who knows? The paraglider trike that Dall-E generated for yesterday could, I guess.

Metal Island is a land where everything is made of metal. The trees are metal. The flowers are metal. The scurrying little animals are metal and… whoa, animals? The animal in question ducks into a pipe and disappears. You realize that you are standing on a maze of pipes, and if you have any hope of catching the metal animal (or whatever, my guess is robo-elf), you’ll need to solve the maze of pipes and figure out where to stand to grab it.

I’m sure I will eventually go back and solve some of these puzzles in Haskell. This one: not so much. This one is all Python and that’s all it will ever be. My use of AI for these later puzzles is near nil. I’m doing them in Python, I’m not trying to describe the problem to an AI so that it will solve it for me.

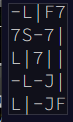
The maze in this puzzle is made out of ASCII art, which uses letters, digits, and typography to “suggest” a maze shape. You can see one above. Not every pipe connects to another pipe. The “S” is the start position, where we saw Robo-Elf (just gonna assume this) duck into the pipe. It itself is also a pipe shape, that can be derived from its surrounding pipes. In this case, it is a “F”, a pipe leading south and east.

The solution for Part 1 is to figure out the number of pipes the Robo-Elf would have to past through to get to the pipe that is furthest from the start position.

First, we need to lay a little groundwork.

Direction = Enum('Direction', ['NORTH', 'EAST', 'SOUTH', 'WEST'])

symbols = { '|' : [Direction.NORTH, Direction.SOUTH], 
            '-' : [Direction.EAST, Direction.WEST],
            'L' : [Direction.NORTH, Direction.EAST],
            'J' : [Direction.NORTH, Direction.WEST],
            '7' : [Direction.SOUTH, Direction.WEST],
            'F' : [Direction.SOUTH, Direction.EAST] }

offsets = { Direction.NORTH : (0, -1),
            Direction.EAST  : (1, 0),
            Direction.SOUTH : (0, 1),
            Direction.WEST  : (-1, 0) }

opposite_offset = { Direction.NORTH : Direction.SOUTH,
                    Direction.EAST  : Direction.WEST,
                    Direction.SOUTH : Direction.NORTH,
                    Direction.WEST  : Direction.EAST }

blocking_direction = { Direction.NORTH : Direction.EAST,
                       Direction.EAST  : Direction.SOUTH,
                       Direction.SOUTH : Direction.WEST,
                       Direction.WEST  : Direction.NORTH }

Inspired by the Haskell solutions I’ve been seeing, I’ve decided to get a little more formal with my Python. Direction is a list of directions, obviously. symbols is a dictionary that takes one of the pipe symbols from the puzzle and matches it with the directions the pipe exits the square it’s on. offsets defines how to transform a position by the direction. opposite_offset just shows which direction is opposite the given direction. And blocking_direction is for part 2, so I’ll get to that in a bit. It is the next direction clockwise from the given direction.

lgrid = None
lvisited = None

def read_data() -> list:
    with open("puzzle10.dat") as f:
        return f.read().splitlines()

def find_start():
    # start position is marked with 'S'.
    return [(row.index('S'), i) for i, row in enumerate(lgrid) if 'S' in row][0]

So here I am saving the grid (the puzzle input) and the visited pipes that determine which pipes are part of the maze (output from part 1) as global variables because I plan to use… caching… and the cache can’t handle mutable types like these two lists.

find_start looks through the grid and returns the coordinates (x,y) of the ‘S’. It’s our start position.

def part1() -> list:
    starting_position = find_start()
    adjacent = find_adjacent(starting_position)
    mice = [move_pos(starting_position, direction) for direction in adjacent]
    visited = [starting_position] + mice
    while True:
        new_mice = [move_pos(mouse, z) for mouse in mice for z in find_adjacent(mouse) if move_pos(mouse, z) not in visited]
        if len(new_mice) < 2:
            break
        visited += new_mice
        mice = new_mice
    return visited

part1 starts at the starting position, and sends mice running in both directions. When a mouse can’t move without hitting a place it’s visited, it returns the list of visited pipes.

This is not the best way to do this. Best way would just be to run a mouse through the pipes in one direction and stop when it returns to start. But that would have meant having to figure out which direction it came in to choose the correct exit, and I didn’t feel like it. It runs pretty slow as a result.

@lru_cache(maxsize=None)
def find_adjacent(pos: tuple) -> list:
    # given the grid and a position (pos), return the offsets of the two orthogonally adjacent squares that point back to the position
    # using symbols and offsets. if no adjacent squares are found, return empty list
    if pos[0] < 0 or pos[1] < 0 or pos[0] >= len(lgrid[0]) or pos[1] >= len(lgrid):
        return []
    symbol = lgrid[pos[1]][pos[0]]
    if symbol not in symbols and symbol != 'S':
        return []
    if symbol in symbols:
        return symbols[lgrid[pos[1]][pos[0]]]
    return [direction for direction in Direction \
            if opposite_offset[direction] in find_adjacent(move_pos(pos, direction))]

Okay, find_adjacent finds the two adjacent symbols that point back at this one. This lets us find out what points back at the starting position so we can tell what symbol it should be. And I use it everywhere else, even though it might be faster to… not, and use one that reads the current symbol.

In order to excuse my sloppy coding, I threw a cache on it, so that the second time it’s asked to find the adjacent pipes for a position, it will just return immediately without calculating it again.

Okay, so that wasn’t so bad, right?

Part 2 just messes the whole thing up.

You, the helper who always seems to be called upon each year to save the elves from themselves, have decided that the Robo-Elf has maybe scurried out of the pipe maze and could be anywhere inside the area surrounded by the maze. Why? I don’t know. It’s something you decided. Don’t blame me, I’m not even there.

Part 2 is to calculate the volume of the area that is within the loop made by the maze.

So in the input, a period (‘.’) denotes empty space. If you look way back up at the start of the post at the sample puzzle input, you won’t see any empty space. But the empty space is implied; it is the space between the pipes.

This is something I did not understand for a very long time. I was only calculating the interiosity of empty spaces, even though the puzzle description made it clear that this was not the correct solution.

The algorithm I used was, you take a point and draw a line connecting it to a point known to be outside the area (i.e., any point outside the grid). You then count the number of intersections with the edge of the polygon. If that count is even, it is outside the shape, otherwise it is inside.

Only one line is necessary, but because of the weird way they define interior points, I decided that a point was inside only if rays cast from all four cardinal directions all indicated it was inside. This was calculation intensive.

@lru_cache(maxsize=None)
def blocked(direction: Direction, pos: tuple) -> bool:
    looking_at = lgrid[pos[1]][pos[0]]
    if looking_at not in symbols:
        return False
    return blocking_direction[direction] in symbols[looking_at]

# cache this
@lru_cache(maxsize=None)
def crossing_count(direction: Direction, pos: tuple) -> int:
    if pos[0] < 0 or pos[1] < 0 or pos[0] >= len(lgrid[0]) or pos[1] >= len(lgrid):
        return 0
    # print ("crossing_count", direction, pos)
    return (1 if pos in lvisited and blocked(direction, pos) else 0) + crossing_count(direction, move_pos(pos, direction))

@lru_cache(maxsize=None)
def is_inside(pos: tuple) -> bool:
    return not any((crossing_count(direction, pos) % 2) == 0 for direction in Direction)

Liberally using caching here. It’s like sugar. Just keep adding more. Eventually it will be sweet enough.

blocked is my special algorithm for deciding whether or not one of our virtual in between points intersected the maze loop. A ray casting north will be blocked if it encounters a symbol that indicates it exits east. A ray casting east, blocked if it finds a south, and so on. I had to work this out on a notepad. I’m not going to copy that out here. It works. How it works is left to you, dear reader / elf helper.

I originally wrote crossing_count to not be recursive, but I wanted to put that cache to work, so I rewrote it to be recursive. This is the ray caster.

And finally, is_inside casts rays in all four directions and returns true if none of them crossed the maze loop an even number of times.

def part2() -> int:
    # count the number of '.' in the grid that are not outside the maze
    return sum(1 for r, row in enumerate(lgrid) for x, c in enumerate(row) if is_inside((x, r)))

def what_symbol_is_s():
    start_pos = find_start()
    adjacent = find_adjacent(start_pos)
    # find symbol matching adjacent value
    for symbol, directions in symbols.items():
        if len(adjacent) == len(set(adjacent + directions)):
            return symbol
    return None

Finally, part2 calls is_inside on every grid position and sums up those that are actually inside. what_symbol_is_s calculates what to replace the ‘S’ symbol in the grid with in order to have it work correctly for part 2.

That’s pretty much it. I saw that other solvers were using flood fill for this. I am not using flood fill.